Guia Matlab
Universidad Politécnica de Madrid
Enunciado:
La derivada de una función f(x) la aproximamos con la siguiente fórmula
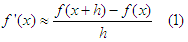
El error de truncamiento viene dado por:
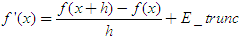
Una Cota del error de truncamiento se obtiene de la expresión:
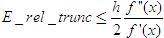
Una cota del error relativo de redondeo cometido al calcular f(x+h)-f(x) en la fórmula (1) se obtiene de la expresión:
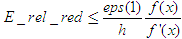
Teniendo en cuenta la relación:
Error numérico total = Error de truncamiento + Error de redondeo
Aplicamos la fórmula a la función f(x)=sen(x) en el punto x=1. Queremos dibujar la gráfica de las cotas de los 3 errores relativos, respecto del valor de h.
El código debe hacer lo siguiente:
- Crear el vector h=10^-n, con n=[0 1 2 ... 20].
- Evaluar la función f'(x)=cos(x) en x=1, utilizando el comando cos( ).
- Evaluar la función (f(x+h)-f(x))/2 en los valores de h, con x=1.
- Evaluar el error absoluto y a partir de él, el error relativo.
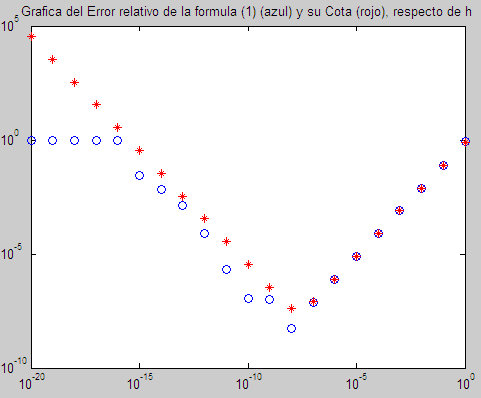
- Representar el error relativo (azul) y la Cota del error numérico total (rojo), respecto de h, en ejes logarítmicos (loglog).
Teniendo en cuenta el resultado de la gráfica, contestar a las siguientes preguntas, comentando los resultados:
- ¿son adecuadas las cotas del error obtenidas?,
- Para h=10-3 ¿cuántas cifras significativas de precisión obtenemos?, ¿y para h=10-14 ?
- ¿para qué h se obtiene el mayor número de cifras significativas de precisión?, ¿cuántas cifras son?
- ¿qué pasa para h<=10-16 ?.
Solución:
[ANEXO ejer2-1.m]
>> ejer2-1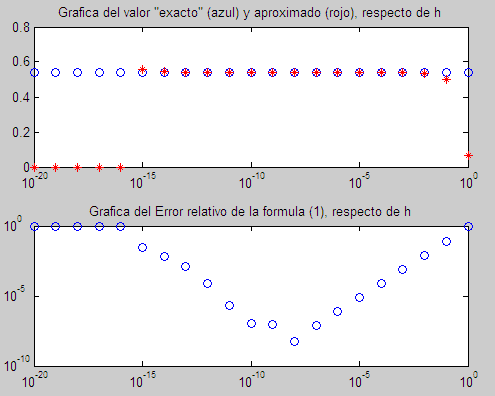
loglog(h,E_rel,'bo'),title('Grafica del Error relativo de la formula (1), respecto de h')
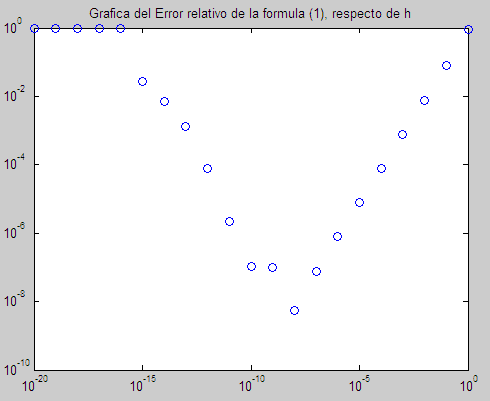
loglog(h,E_rel,'bo',h,E_rel_cota,'r*'),title('Grafica del Error relativo de la formula (1) (azul) y su Cota (rojo), respecto de h')