Enunciado:


La función x=solve_U(U,b), implementa la resolución de un sistema triangular superior Ux=b, utilizando el método sustitución regresiva. Los argumentos de entrada son la matriz triangular superior U y el vector b. El argumento de salida es x. Si la matriz de entrada es singular, x será un vector de NaN.

 La siguiente función, x=solve_L(L,b), implementa la resolución de un sistema triangular inferior Lx=b.

function x=solve_L(L,b)
% Resuelve el sistema triangular inferior Lx=b
% Si la matriz L es singular devuelve NaN
 n=length(b); x=NaN*b;
D=diag(L); % Extraigo la diagonal de U
 determinante=prod(D); % Productorio de la diagonal
 if determinante==0, return; end % Compruebo si U es singular
% Resolvemos Lx=b utilizando sustitución progresiva
 for i=1:n
x(i)=(b(i)-sum(L(i,1:i-1).*x(1:i-1)'))/D(i);
end

Si la matriz U es triangular superior y la matriz L es triangular inferior con 1?s en la diagonal, se puede reducir el tamaño de memoria utilizado almacenando las matrices U y L en una única matriz L_U:



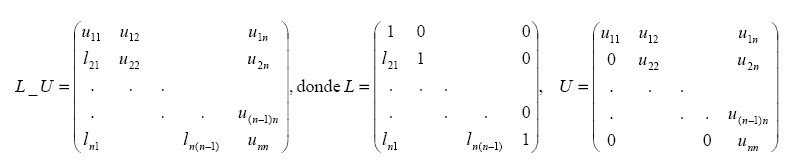
Combinar las dos funciones anteriores en una tercera,
x=solve_LU(L_U,b), que resuelva el sistema LUx=b, donde L_U contiene las matrices L y U. Recordar que la función debe resolver dos sistemas:

Ly=b donde L contiene los elementos de la triangular inferior de L_U y 1's en su diagonal,
Ux=y donde U contiene los elementos de la triangular superior de L_U e y es la solución del sistema anterior.
Comprobar la función resolviendo LUx=b, ejecutando x=solve_LU(L_U,b), donde

 L=[1 0 0 0 0;7 1 0 0 0;2 7 1 0 0;0 9 7 1 0;7 3 6 4 1]
U=[9 3 2 0 7;0 6 9 6 4;0 0 7 8 2;0 0 0 2 2;0 0 0 0 3]
L_U=[9 3 2 0 7;7 6 9 6 4;2 7 7 8 2;0 9 7 2 2;7 3 6 4 3]
b=[35;303;522;858;763];

La solución es x= [0 1 2 3 4]'.
Calcular el valor de la matriz A=L*U. Comprobar que x es la solución de Ax=b. Calcular el vector residuo.

Solución:


function x=solve_LU(L_U,b)
% Resuelve el sistema LUx=b
%
n=length(b); x=NaN*b;
D=diag(L_U); % Extraigo la diagonal de U
determinante=prod(D); % Productorio de la diagonal
if determinante==0, return; end %
Compruebo si U es singular
% Resolvemos Ux=b utilizando sustitución regresiva

L=zeros(n);
U=zeros(n);

%Extraigo la matriz U de la matriz L_U
for k=1:n
U(k,k:n)=L_U(k,k:n);
end
L=L_U-U+diag(ones(5,1));
y=solve_L(L,b);
x=solve_U(U,y);

% Comprobacion
>> A=L*U

A =
  9    3   2  0   7
  63  27  23  6  53
  18  48  74  50  44
  0  54  130  112  52
  63  39  83  74  84

>> A*x

ans =
35
303
522
858
763