EJEMPLO 1: RESOLUCIÓN DE SISTEMAS TRIANGULARES

 

La función x=solve_U(U,b), implementa la resolución de un sistema triangular superior Ux=b, utilizando el método sustitución regresiva. Los argumentos de entrada son la matriz triangular superior U y el vector b. El argumento de salida es x. Si la matriz de entrada es singular, x será un vector de NaN.

Por otra parte, la función x=solve_L(L,b). implementa la resolución de un sistema triangular inferior Lx=b.

 [ANEXO solve_U.m solve_L.m]

Si la matriz U es triangular superior y la matriz L es triangular inferior con 1’s en la diagonal, se puede reducir el tamaño de memoria utilizado almacenando las matrices U y L en una única matriz L_U:



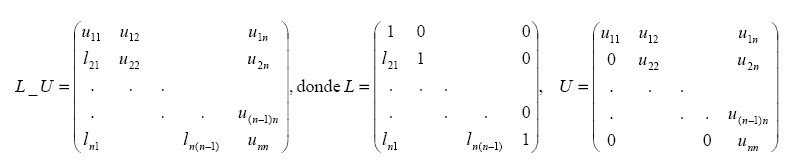
• Combinar las dos funciones anteriores en una tercera,
x=solve_LU(L_U,b), que resuelva el sistema LUx=b, donde L_U contiene las matrices L y U. Recordar que la función debe resolver dos sistemas:

Ly=b donde L contiene los elementos de la triangular inferior de L_U y 1’s en su diagonal,
Ux=y donde U contiene los elementos de la triangular superior de L_U e y es la solución del sistema anterior.
Comprobar la función resolviendo LUx=b, ejecutando x=solve_LU(L_U,b), donde

 L=[1 0 0 0 0;7 1 0 0 0;2 7 1 0 0;0 9 7 1 0;7 3 6 4 1]
U=[9 3 2 0 7;0 6 9 6 4;0 0 7 8 2;0 0 0 2 2;0 0 0 0 3]
L_U=[9 3 2 0 7;7 6 9 6 4;2 7 7 8 2;0 9 7 2 2;7 3 6 4 3]
b=[35;303;522;858;763];

La solución es x= [0 1 2 3 4]'.
Calcular el valor de la matriz A=L*U. Comprobar que x es la solución de Ax=b. Calcular el vector residuo.


[Solución]

[Terminar]